狄克斯拉特算法(Dijkstra)
今天看《算法图解》这本书,讲到狄克斯拉特算法(Dijkstra)。感觉挺有意思的,所以将书中的小例子用python代码实现,然后记录一下。
狄克斯拉特算法(Dijkstra)
首先,讲讲什么是狄克斯拉特算法。狄克斯拉特算法是解决从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。
图
那么什么是有权图呢?在将这个之前,我们先来讲什么是图。
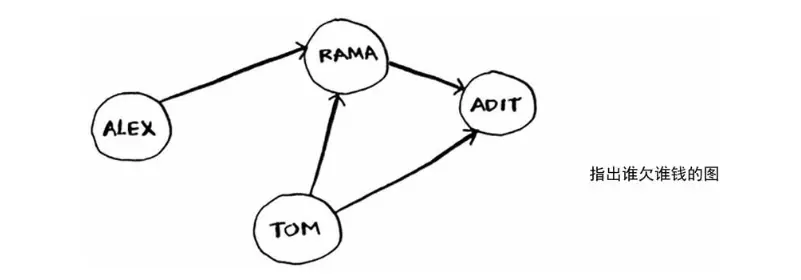
Alex欠Rama的钱,Tom欠Rama和Adit的钱,图由节点和边组成。一个节点可能与众多节点直接相连,这些节点被称为邻居。在前面的欠钱图中,Rama是Alex的邻居。Adit不是Alex的邻居,因为他们不直接相连。但Adit既是Rama的邻居,又是Tom的邻居。
加权图
那么加权图就是在每条边上都有权重的图。就像下面这个图片里标注的一样。去每个不同的节点所消耗的时间。
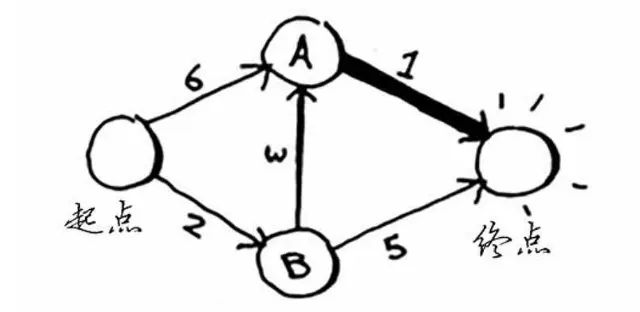
算法具体步骤
狄克斯特拉算法包含4个步骤。
- 找出最便宜的节点,即可在最短时间内前往的节点。
- 对于该节点的邻居,检查是否有前往它们的更短路径,如果有,就更新其开销。
- 重复这个过程,直到对图中的每个节点都这样做了。
- 计算最终路径。
步骤比较抽象,下面举个具体的例子。
例子
这是Rama,想拿一本乐谱换架钢琴。
Alex说:“这是我最喜欢的乐队Destroyer的海报,我愿意拿它换你的乐谱。如果你再加5美元,还可拿乐谱换我这张稀有的Rick Astley黑胶唱片。
”Amy说:“哇,我听说这张黑胶唱片里有首非常好听的歌曲,我愿意拿我的吉他和架子鼓换这张海报和黑胶唱片。”
Beethoven惊呼:“我一直想要吉他,我愿意拿我的钢琴换Amy的吉他或架子鼓。”太好了!只要再花一点点钱,Rama就能拿乐谱换架钢琴。
现在他需要确定的是,如何花最少的钱实现这个目标。我们来绘制一个图,列出大家的交换意愿。
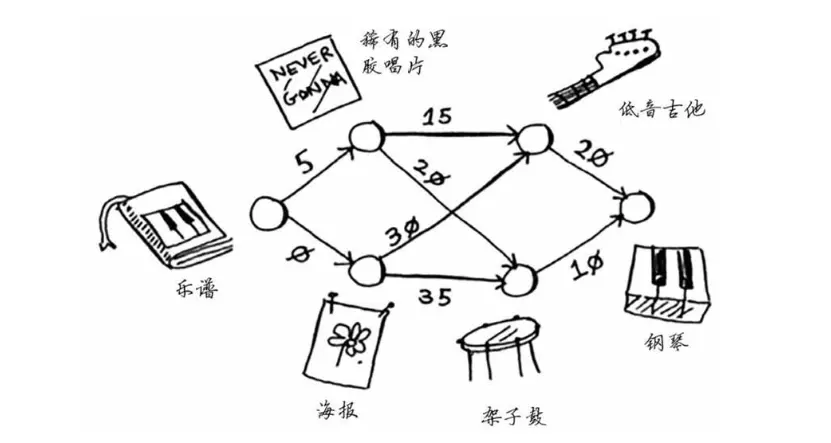
首先我们为上面的图建立数据模型,我们可以用python的字典存储上面的数据
# 图
graph = {}
graph['乐谱'] = {}
graph['乐谱']['海报'] = 0
graph['乐谱']['黑胶唱片'] = 5
graph['海报'] = {}
graph['海报']['吉他'] = 30
graph['海报']['架子鼓'] = 35
graph['黑胶唱片'] = {}
graph['黑胶唱片']['吉他'] = 15
graph['黑胶唱片']['架子鼓'] = 20
graph['吉他'] = {}
graph['吉他']['钢琴'] = 20
graph['架子鼓'] = {}
graph['架子鼓']['钢琴'] = 10
graph['钢琴'] = {}
我们再建立一个花费的字典,从乐谱开始,没有和乐谱直接相连的就是无穷远,和乐谱相连的就是相应的花费。
infinity = float("inf") # 表示无穷
# 花费
costs = {}
costs['黑胶唱片'] = 5
costs['海报'] = 0
costs['吉他'] = infinity
costs['架子鼓'] = infinity
costs['钢琴'] = infinity
我们在建立一个父节点字典,后面我们要更新花费字典和父节点字典。
# 父节点
parents = {}
parents['海报'] = '乐谱'
parents['黑胶唱片'] = '乐谱'
parents['吉他'] = None
parents['架子鼓'] = None
parents['钢琴'] = None
再创建一个已处理的节点列表,防止重复处理
# 已处理过的节点
processed = []
上面的步骤中,第一步是:找出最便宜的节点。从乐谱开始,最便宜的节点就是海报了,不需要额外支出任何花费。我们来定义一个函数,可以从花费表里获取到最便宜的节点
# 找到未处理节点中,开销最小的节点
def find_lowest_cost_node(_costs):
# 默认为无穷
min_cost = infinity
lowest_node = None
for c in _costs:
# 过滤已处理的
if c not in processed:
if _costs[c] < min_cost:
min_cost = _costs[c]
lowest_node = c
return lowest_node
下一步就是获取最小节点邻居的节点,看看是否有通往他们花费最小的路径,有的话更新花费表和父节点表。然后重复这个过程,看最终代码
node = find_lowest_cost_node(costs)
while node is not None:
cost = costs[node]
# 获取邻居节点
neighbors = graph[node]
for n in neighbors.keys():
new_cost = cost + neighbors[n]
if new_cost < costs[n]:
# 更新花销表和父节点表
costs[n] = new_cost
parents[n] = node
# 处理完后加入到已处理过列表
processed.append(node)
# 找到未处理节点中,开销最小的节点
node = find_lowest_cost_node(costs)
我们输出花销表和父节点表
print(costs)
print(parents)
{'黑胶唱片': 5, '海报': 0, '吉他': 20, '架子鼓': 25, '钢琴': 35}
{'海报': '乐谱', '黑胶唱片': '乐谱', '吉他': '黑胶唱片', '架子鼓': '黑胶唱片', '钢琴': '架子鼓'}
可以看到,兑换到钢琴,最低的花销是35。
路径可以从钢琴倒推回去,钢琴的父节点是架子鼓,架子鼓的父节点是黑胶唱片,以此循环,最终结果为:钢琴<-架子鼓<-黑胶唱片<-乐谱