CRC循环冗余校验手动计算

什么是CRC循环冗余校验呢？我们先来看看百度百科的解释。

循环冗余校验（英语：Cyclic redundancy check，通称“CRC”）是一种根据网上数据包或计算机文件等数据产生简短固定位数校验码的一种散列函数，主要用来检测或校验数据传输或者保存后可能出现的错误。生成的数字在传输或者存储之前计算出来并且附加到数据后面，然后接收方进行检验确定数据是否发生变化。一般来说，循环冗余校验的值都是32位的整数。由于本函数易于用二进制的计算机硬件使用、容易进行数学分析并且尤其善于检测传输通道干扰引起的错误，因此获得广泛应用。此方法是由W. Wesley Peterson于1961年发表。

简单来说CRC就是用在数据链路层，用来校验数据报有没有丢失或错误的一种方法。

这篇文章的重点在于对CRC校验的手动计算，原理部分比较复杂，加上个人水平有限，有兴趣的读者请自行了解。

例题

首先看例题，我们通过例题来讲解如何手动计算

【例题】假设CRC编码采用的生成多项式为$G(x)=x^4+x+1$，请为位串10111001进行CRC编码。

多项式

使用CRC时，通信双方会协商生成一个多项式，在发送方，利用生成多项式对信息多项式做模2除生成校验码。在接受方利用生成多项式对收到的编码多项式做模2除检测和确定错误位置。

应满足以下条件：

• 生成多项式的最高位和最低位必须为1。

• 当被传送信息（CRC码）任何一位发生错误时，被生成多项式做模2除后应该使余数不为0。

• 不同位发生错误时，应该使余数不同。

• 对余数继续做模2除，应使余数循环。

在CRC校验中，多项式可以表示为：$(\sum_{i=1}^jC_ix^i)+1,C=0,1$

列如：$1 \times x^4 + 0 \times x^3 + 0\times x^2 + 1 \times x^1 + 1 \times x^0$

可简写为：$x^4+x+1$

CRC中用到的除数，正是由多项式的各项系数组成，从上面可得：10011

考试中，多项式一般都是简写形式，我们要根据简写的多项式，写出CRC除数。

原数据末端加0

我们根据多项式的最高次数来为原数据串末尾补0，例题中最高次数是4，那么补零后的结果是：101110010000

做除法

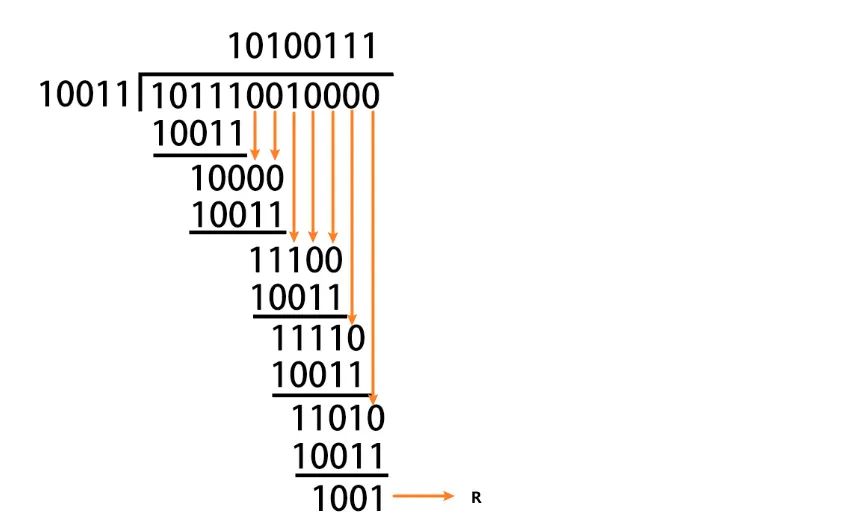
原数据尾端加0后，除以10011，因为除数为5位，所以在第5位的时候商1，然后做模2加法运算，第一次运算余数为100，不足5位将上面的数取下来一位，然后商0，变成1000还是不够五位，再取一位变成10000，够五位了，商1。接下来的运算一位类推。

所谓“模2加法”就是0和1之间的加法，其中0+0 =0，1+0 =0+1 =1，1+1=0(!)。这种运算在通信和计算机上是常用的，而且并不神秘．你可以把0和1分别想成是“偶数”和“奇数”，那么前两个式子分别代表：偶数加偶数等于偶数，奇数加偶数等于奇数，而式1+1=0就是奇数加奇数等于偶数．对于任意多个数a1，a2，…，am（每个都是0或1），可以把它们做模2加法a1+a2+…+am。不难看出，当这m个数中有奇数个1时，结果为1，否则结果为0。

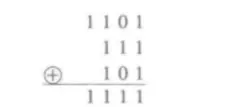
对二进制数定义模2加法，规则非常简单：即每个数位上分别作模2加法，由此得出一个新的二进制数，例如[ 1101]+[111]+[101]=[1111]，写成算式为

最终结果

通过上面的运算，获得余数为1001，然后将被除数和余数进行相加。$101110010000+1001=101110011001$

这里有一点要注意，这道题的余数刚好是4位，如果不足数位如10，需要在前面补足到4位，0010，然后再进行相加，余数的位数，根据多项式最高次数决定。

所以最终结果是：101110011001

总结

总共分为4步

1. 分析多项式，将多项式的系数取出来，作为之后运算的除数，多项式的最高次作为原数据补0的个数。
2. 在原数据尾端补0，0的个数就是多项式的最高次的次数
3. 然后将补0的原数据与第一步的多项式除数相除，取余数
4. 将上一步的余数（不足需前面补0）与补0后的原数据向加

参考资料

模2运算

自考04741 计算机网络原理，CRC例题解析